확률 및 통계 기초 이해하기: 확률 분포
확률과 통계는 다양한 분야에서 활용되는 중요한 도구입니다. 이번 글에서는 확률 분포에 대해 알아보겠습니다. 이산 확률 분포와 연속 확률 분포로 나누어 각각 이항 분포, 포아송 분포, 정규 분포, 균일 분포를 설명하겠습니다.
1. 이산 확률 분포
이산 확률 분포는 이산형 확률 변수가 취할 수 있는 값과 각 값이 발생할 확률을 나타냅니다. 이산 확률 변수는 셀 수 있는 값을 가집니다.
이항 분포
이항 분포는 각 시행이 성공 또는 실패 두 가지 결과만을 가지는 독립적인 시행이 n번 반복될 때, 성공 횟수를 나타내는 확률 분포입니다. 각 시행에서 성공할 확률을 p, 실패할 확률을 1−p라고 합니다.
이항 분포의 확률 질량 함수(PMF)는 다음과 같습니다.

여기서 이항 계수는 다음과 같이 계산됩니다.

예제: 이항 분포
동전을 10번 던져 앞면이 나올 확률을 구해보겠습니다. 동전을 던질 때 앞면이 나올 확률 p는 0.5입니다.
- 시행 횟수 n = 10
- 성공 확률 p = 0.5
- 성공 횟수 k = 6

따라서, 10번 던졌을 때 앞면이 6번 나올 확률은 약 0.205입니다.
포아송 분포
포아송 분포는 일정한 시간 또는 공간 내에 발생하는 사건의 수를 나타내는 이산 확률 분포입니다. 사건이 발생하는 평균 횟수를 λ라고 합니다.
포아송 분포의 확률 질량 함수(PMF)는 다음과 같습니다.

여기서 e는 자연 로그의 밑입니다.
예제: 포아송 분포
한 시간 동안 평균적으로 5번의 전화가 걸려오는 콜센터에서, 한 시간 동안 3번의 전화가 걸려올 확률을 구해보겠습니다.
- 평균 횟수 λ = 5
- 사건의 수 k = 3
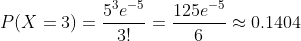
따라서, 한 시간 동안 3번의 전화가 걸려올 확률은 약 0.1404입니다.
2. 연속 확률 분포
연속 확률 분포는 연속형 확률 변수가 취할 수 있는 값의 범위와 그 값들이 분포하는 방식에 대해 설명합니다. 연속 확률 변수는 연속적인 값을 가집니다.
정규 분포
정규 분포는 가장 널리 알려진 연속 확률 분포로, 데이터가 평균을 중심으로 대칭적으로 분포하는 종 모양의 곡선을 나타냅니다. 평균을 μ, 표준 편차를 σ라고 합니다.
정규 분포의 확률 밀도 함수(PDF)는 다음과 같습니다.

예제: 정규 분포
평균이 0이고 표준 편차가 1인 정규 분포(표준 정규 분포)를 가정합니다. 이 분포에서 x가 -1과 1 사이에 있을 확률을 구해보겠습니다.

이 확률은 표준 정규 분포표를 통해 약 0.6826임을 알 수 있습니다.
균일 분포
균일 분포는 확률 변수가 일정 범위 내에서 균일하게 분포하는 것을 나타냅니다. 구간 [a, b] 내에서 모든 값이 동일한 확률을 가집니다.
균일 분포의 확률 밀도 함수(PDF)는 다음과 같습니다.

예제: 균일 분포
0과 10 사이에서 균일하게 분포하는 확률 변수를 가정합니다. 이때, 3과 7 사이에 있을 확률을 구해보겠습니다.

따라서, 0과 10 사이의 균일 분포에서 3과 7 사이에 있을 확률은 0.4입니다.
마무리
확률 분포는 데이터가 어떻게 분포되어 있는지를 설명하는 중요한 개념입니다. 이산 확률 분포에는 이항 분포와 포아송 분포가 있으며, 연속 확률 분포에는 정규 분포와 균일 분포가 포함됩니다. 이러한 분포를 이해하면 다양한 확률 문제를 더 쉽게 해결할 수 있습니다. 다음 글에서는 이러한 기본 개념을 바탕으로 더 복잡한 확률 이론과 통계 기법에 대해 알아보겠습니다.
궁금한 점이 있거나 추가 설명이 필요한 부분이 있다면 댓글로 남겨주세요! 함께 학습해 나갑시다.
'인공지능학 > 확률 및 통계' 카테고리의 다른 글
| [확률 및 통계] 6. 통계적 추론 (0) | 2024.06.29 |
|---|---|
| [확률 및 통계] 5. 기대값과 분산 (0) | 2024.06.23 |
| [확률 및 통계] 3. 조건부 확률과 독립성 (0) | 2024.06.15 |
| [확률 및 통계] 2. 확률의 정의와 법칙 (0) | 2024.06.15 |
| [확률 및 통계] 1. 기본 개념 이해 (0) | 2024.06.14 |



