[확률 및 통계] 6. 통계적 추론

확률 및 통계 기초 이해하기: 통계적 추론

통계적 추론은 모집단의 특성을 표본을 통해 추정하고 검정하는 과정입니다. 이는 데이터 분석에서 매우 중요한 부분으로, 모집단의 특성을 이해하고 예측하는 데 필수적입니다. 이번 글에서는 표본과 모집단, 추정과 가설 검정에 대해 알아보겠습니다.

1. 표본과 모집단

표본과 모집단의 정의

• 모집단 (Population): 연구나 분석의 대상이 되는 전체 집단을 의미합니다. 예를 들어, 특정 도시의 모든 주민, 특정 제품의 모든 생산품 등이 모집단이 될 수 있습니다.
• 표본 (Sample): 모집단에서 추출된 일부 요소들로 구성된 집단을 의미합니다. 표본은 모집단을 대표할 수 있어야 하며, 이를 통해 모집단의 특성을 추정할 수 있습니다.

 

표본평균 (Sample Mean)

표본평균은 표본 데이터의 평균을 나타내며, 모집단 평균의 추정치로 사용됩니다.

표본평균 는 다음과 같이 계산됩니다.

 

​

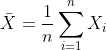
여기서 n은 표본의 크기, Xi는 표본의 각 관측값입니다.

 

예제: 표본평균

6명의 학생의 시험 점수가 85, 90, 78, 92, 88, 84일 때, 표본평균을 구해보겠습니다.

 

따라서, 이 표본의 평균 점수는 약 86.17입니다.

 

 

표본분산 (Sample Variance)

표본분산은 표본 데이터의 분산을 나타내며, 모집단 분산의 추정치로 사용됩니다. 표본분산 는 다음과 같이 계산됩니다.

 

여기서 n은 표본의 크기, Xi는 표본의 각 관측값, 는 표본평균입니다.

 

예제: 표본분산

위 예제의 시험 점수를 사용하여 표본분산을 구해보겠습니다.

• 표본평균

• 각 관측값 Xi와 표본평균의 차이 제곱의 합:

 

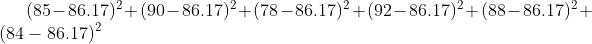
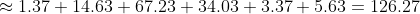
따라서, 이 표본의 분산은 약 25.25입니다.

 

 

2. 추정과 가설 검정

 

점추정 (Point Estimation)

점추정은 모집단의 모수를 하나의 값으로 추정하는 방법입니다. 예를 들어, 모집단 평균 μ에 대한 점추정치는 표본평균 입니다.

 

 

구간추정 (Interval Estimation)

구간추정은 모집단의 모수를 특정 신뢰 수준 하에 일정 범위(구간)로 추정하는 방법입니다. 이는 점추정의 불확실성을 반영하여 보다 신뢰할 수 있는 추정치를 제공합니다. 구간추정의 대표적인 예는 신뢰구간입니다.

 

 

신뢰구간 (Confidence Interval)

신뢰구간은 모집단의 모수가 특정 구간에 포함될 확률을 나타냅니다. 예를 들어, 95% 신뢰구간은 모집단의 모수가 95% 확률로 이 구간 내에 있을 것이라는 의미입니다. 표본평균의 신뢰구간은 다음과 같이 계산됩니다.

 

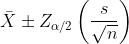
여기서 는 표준 정규분포의 백분위수, s는 표본표준편차, n은 표본의 크기입니다.

 

예제: 신뢰구간

6명의 학생의 시험 점수의 95% 신뢰구간을 구해보겠습니다. 앞서 계산한 표본평균 , 표본표준편차 s ≈ 5.02, 표본의 크기 n = 6입니다. 95% 신뢰구간에서 입니다.

 

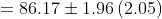
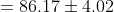
따라서, 95% 신뢰구간은 (82.15, 90.19)입니다.

 

 

가설검정 (Hypothesis Testing)

가설검정은 모집단의 모수에 대한 가설을 설정하고, 표본 데이터를 통해 이를 검증하는 과정입니다. 가설검정의 기본 절차는 다음과 같습니다.

1. **귀무가설(H0)**과 대립가설(H1) 설정
2. 유의 수준(α) 설정
3. 검정 통계량 계산
4. 기각역 결정 및 결론 도출

 

예제: 가설검정

한 학교의 평균 시험 점수가 85점이라고 주장하는 귀무가설(H0: μ = 85)을 검증해보겠습니다. 표본의 평균 점수는 86.17, 표본표준편차는 5.02, 표본 크기는 6입니다. 유의 수준은 0.05로 설정합니다.

• 귀무가설(H0): μ = 85
• 대립가설(H1): μ ≠ 85

검정 통계량은 다음과 같이 계산됩니다.

 

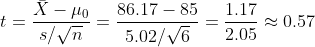
유의 수준 0.05에서 양측 검정의 기각역은 입니다. 검정 통계량 t ≈ 0.57은 기각역에 포함되지 않으므로, 귀무가설을 기각하지 않습니다.

 

 

마무리

통계적 추론은 표본을 통해 모집단의 특성을 추정하고 검증하는 과정입니다. 표본평균과 표본분산을 통해 모집단의 모수를 추정하고, 점추정과 구간추정을 통해 보다 신뢰할 수 있는 추정치를 제공합니다. 가설검정을 통해 모집단에 대한 가설을 검증함으로써 데이터 분석의 정확성을 높일 수 있습니다. 이러한 기초 개념을 이해하면 더 복잡한 통계 분석도 쉽게 접근할 수 있습니다.

궁금한 점이 있거나 추가 설명이 필요한 부분이 있다면 댓글로 남겨주세요! 함께 학습해 나갑시다.