확률 및 통계 기초 이해하기: 확률의 정의와 법칙
확률과 통계는 다양한 분야에서 활용되는 중요한 도구입니다. 이번 글에서는 확률의 기본 정의와 법칙에 대해 알아보겠습니다. 확률의 공리적 정의와 균일 확률을 통해 기본 개념을 이해하고, 합의 법칙, 곱의 법칙, 여사건의 확률 법칙을 통해 확률 계산의 기초를 다져보겠습니다.
1. 확률의 기본 정의
확률의 공리적 정의
확률의 공리적 정의는 다음 세 가지 기본 공리에 기반합니다.
- 비음성성 (Non-negativity): 모든 사건 A에 대해, 그 사건의 확률 P(A)는 0 이상입니다. 0 ≤ P(A)
- 전체 확률 (Total Probability): 표본 공간 S의 확률은 1입니다. P(S) = 1
- 가법성 (Additivity): 서로 배반적인 (동시에 일어날 수 없는) 두 사건 A와 B에 대해, 이들의 합집합의 확률은 각 사건의 확률의 합과 같습니다. P(A∪B) = P(A) + P(B) (if A∩B = ∅)
이 세 가지 공리를 바탕으로, 확률 이론의 다양한 법칙과 정리가 유도됩니다.
균일 확률
균일 확률은 표본 공간의 모든 근원 사건이 동일한 확률을 가지는 경우를 의미합니다. 예를 들어, 동전을 던지거나 주사위를 굴리는 경우가 이에 해당합니다. 균일 확률에서는 사건 A의 확률을 다음과 같이 계산할 수 있습니다.
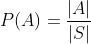
여기서 ∣A∣는 사건 A에 속하는 경우의 수, ∣S∣는 표본 공간 S의 전체 경우의 수입니다.
2. 확률 법칙
합의 법칙 (Law of Addition)
합의 법칙은 두 사건 A와 B의 합집합의 확률을 구할 때 사용됩니다. 두 사건이 배반 사건이 아닐 경우, 두 사건의 교집합을 빼주어야 중복을 제거할 수 있습니다.
- 서로 배반적인 경우 : P(A∪B) = P(A) + P(B)
- 서로 배반적이지 않은 경우 : P(A∪B) = P(A) + P(B) − P(A∩B)
예제: 합의 법칙
주사위를 굴려서 홀수가 나올 확률과 3 이상의 숫자가 나올 확률을 구해보겠습니다.
- 홀수의 사건 A: {1, 3, 5}
- 3 이상의 숫자의 사건 : {3, 4, 5, 6}
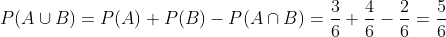
곱의 법칙 (Law of Multiplication)
곱의 법칙은 두 사건 A와 B가 동시에 일어날 확률을 구할 때 사용됩니다. 두 사건이 독립적인 경우와 아닌 경우로 나누어집니다.
- 독립적인 경우 : P(A∩B) = P(A)⋅ P(B)
- 독립적이지 않은 경우 : P(A∩B) = P(A)⋅ P(B∣A)
여기서 P(B∣A)는 사건 A가 일어난 후 사건 B가 일어날 조건부 확률입니다.
예제: 곱의 법칙
주사위를 두 번 굴려 첫 번째에서 3이 나오고, 두 번째에서 5가 나올 확률을 구해보겠습니다.

여사건의 확률 법칙 (Complement Rule)
여사건은 사건 A가 일어나지 않을 확률을 의미합니다. 이는 전체 확률에서 사건 A의 확률을 뺀 값과 같습니다.

예제: 여사건의 확률 법칙
주사위를 굴려서 4가 나오지 않을 확률을 구해보겠습니다.
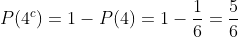
마무리
확률의 기본 정의와 법칙을 이해하는 것은 확률 이론의 기초를 다지는 중요한 단계입니다. 확률의 공리적 정의와 균일 확률을 통해 기본 개념을 이해하고, 합의 법칙, 곱의 법칙, 여사건의 확률 법칙을 통해 다양한 확률 문제를 해결할 수 있습니다.
궁금한 점이 있거나 추가 설명이 필요한 부분이 있다면 댓글로 남겨주세요! 함께 학습해 나갑시다.
'인공지능학 > 확률 및 통계' 카테고리의 다른 글
| [확률 및 통계] 6. 통계적 추론 (1) | 2024.06.29 |
|---|---|
| [확률 및 통계] 5. 기대값과 분산 (2) | 2024.06.23 |
| [확률 및 통계] 4. 확률 분포 (0) | 2024.06.15 |
| [확률 및 통계] 3. 조건부 확률과 독립성 (1) | 2024.06.15 |
| [확률 및 통계] 1. 기본 개념 이해 (0) | 2024.06.14 |



