확률 및 통계 기초 이해하기: 경우의 수, 순열과 조합, 사건과 표본 공간
확률과 통계는 다양한 분야에서 활용되는 중요한 도구입니다. 확률의 기본 개념을 이해하는 것은 복잡한 통계 분석의 기초가 됩니다. 이번 글에서는 경우의 수, 순열과 조합, 사건과 표본 공간에 대해 알아보겠습니다.
1. 경우의 수, 순열과 조합
경우의 수는 어떤 일이 일어날 수 있는 가능한 모든 방법의 수를 의미합니다. 이는 확률 계산의 기본 개념 중 하나로, 모든 가능한 경우를 세는 것이 기본입니다.
예제: 경우의 수
하나의 주사위를 던질 때 나올 수 있는 눈의 경우의 수는 6입니다. 이는 주사위가 1부터 6까지의 숫자를 갖기 때문입니다.
순열 (Permutation)
순열은 서로 다른 n개의 물건 중에서 r개를 택하여 일렬로 나열하는 것을 의미합니다. 이는 순서가 중요할 때 사용됩니다.
순열의 수는 다음과 같이 계산할 수 있습니다.
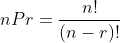
여기서, n!은 n의 팩토리얼로, n부터 1까지의 모든 자연수의 곱입니다.
예제: 순열
4개의 숫자 1, 2, 3, 4에서 3개의 숫자를 선택하여 나열하는 방법의 수를 구해보겠습니다.

조합 (Combination)
조합은 서로 다른 n개의 물건 중에서 순서를 고려하지 않고 r개를 선택하는 것을 의미합니다.
조합의 수는 다음과 같이 계산할 수 있습니다.

예제: 조합
4개의 숫자 1, 2, 3, 4에서 2개의 숫자를 선택하는 방법의 수를 구해보겠습니다.
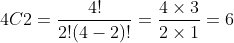
2. 사건과 표본 공간
확률론에서 사건과 표본 공간은 중요한 개념입니다.
사건 (Event)
사건은 실험이나 관찰에서 발생할 수 있는 결과의 집합을 의미합니다. 예를 들어, 동전을 던졌을 때 앞면이 나오는 것이 하나의 사건이 될 수 있습니다.
표본 공간 (Sample Space)
표본 공간은 실험에서 발생할 수 있는 모든 가능한 결과들의 집합을 의미합니다. 표본 공간을 S로 나타냅니다.
예제: 사건과 표본 공간
동전 두 개를 던졌을 때의 표본 공간을 구해보겠습니다.
S={(앞,앞),(앞,뒤),(뒤,앞),(뒤,뒤)}
여기서, 각 쌍은 하나의 근원 사건 (elementary event)입니다. 예를 들어, 첫 번째 동전이 앞면, 두 번째 동전이 뒷면인 사건은 (앞, 뒤)로 표현됩니다.
사건의 예
동전 두 개를 던졌을 때 적어도 하나의 동전이 앞면인 사건 A는 다음과 같이 나타낼 수 있습니다.
A={(앞,앞),(앞,뒤),(뒤,앞)}
마무리
경우의 수, 순열과 조합, 사건과 표본 공간은 확률 및 통계의 기본 개념을 이해하는 데 필수적인 요소들입니다. 이 기초 개념들을 탄탄히 다지면 더 복잡한 확률 문제도 쉽게 접근할 수 있을 것입니다. 앞으로의 글에서는 이 개념들을 바탕으로 더 복잡한 확률 이론과 통계 기법에 대해 알아보겠습니다.
이해가 되지 않는 부분이 있거나 추가적으로 궁금한 사항이 있으면 댓글로 남겨주세요. 함께 공부해 나갑시다!
'인공지능학 > 확률 및 통계' 카테고리의 다른 글
| [확률 및 통계] 6. 통계적 추론 (1) | 2024.06.29 |
|---|---|
| [확률 및 통계] 5. 기대값과 분산 (2) | 2024.06.23 |
| [확률 및 통계] 4. 확률 분포 (0) | 2024.06.15 |
| [확률 및 통계] 3. 조건부 확률과 독립성 (1) | 2024.06.15 |
| [확률 및 통계] 2. 확률의 정의와 법칙 (2) | 2024.06.15 |



