회귀분석의 이해
회귀분석은 기계학습에서 가장 기본적이고 중요한 기법 중 하나로, 연속적인 변수를 예측하는 데 사용됩니다. 이번 글에서는 회귀분석의 개요, 선형회귀분석의 기본 이해, 경사하강법, 그리고 선형회귀모델의 파라미터 추정과 최소제곱법, 파라미터 구간추정과 가설 검정, 정규화 모델에 대해 알아보겠습니다.
회귀분석의 개요
회귀분석 : 회귀분석은 독립 변수와 종속 변수 사이의 관계를 모델링하는 기법입니다. 주로 예측 모델을 만들거나 변수들 간의 관계를 이해하는 데 사용됩니다. 회귀분석의 주요 목표는 데이터로부터 함수의 형태를 추정하여 새로운 데이터를 예측하는 것입니다.
종류
- 단순 회귀분석 : 하나의 독립 변수와 하나의 종속 변수 간의 관계를 모델링합니다.
- 다중 회귀분석 : 여러 독립 변수와 하나의 종속 변수 간의 관계를 모델링합니다.
선형회귀분석의 기본 이해
선형회귀분석 : 선형회귀분석은 종속 변수와 독립 변수 간의 선형 관계를 모델링합니다. 이 모델은 다음과 같은 형태를 가집니다.

여기서
- y는 종속 변수
- x는 독립 변수
 는 절편
는 절편 는 기울기 (회귀 계수)
는 기울기 (회귀 계수)- ϵ은 오차 항
목표 : 회귀 계수 와
와  을 추정하여 데이터에 가장 잘 맞는 직선을 찾는 것입니다.
을 추정하여 데이터에 가장 잘 맞는 직선을 찾는 것입니다.
경사하강법
경사하강법 (Gradient Descent) : 경사하강법은 회귀 계수를 최적화하기 위해 사용되는 알고리즘입니다. 비용 함수(손실 함수)를 최소화하는 방향으로 회귀 계수를 업데이트합니다.
비용 함수 : 선형회귀에서 자주 사용되는 비용 함수는 평균 제곱 오차(MSE)입니다.
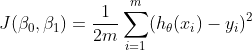
여기서
 는 예측 값
는 예측 값 는 실제 값
는 실제 값- m은 데이터 포인트의 수
경사하강법 알고리즘
1. 초기 회귀 계수 설정

2. 비용 함수의 기울기 계산
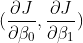
3. 회귀 계수 업데이트


4. 수렴할 때까지 반복
여기서 α는 학습률입니다.
선형회귀모델
파라미터 추정과 최소제곱법
최소제곱법 (Ordinary Least Squares, OLS) : 최소제곱법은 선형회귀 모델의 회귀 계수를 추정하는 가장 일반적인 방법입니다. 잔차 제곱합을 최소화하여 회귀 계수를 추정합니다.
잔차 제곱합 :

여기서 는 예측 값입니다.
는 예측 값입니다.
OLS 해법 :


여기서 와
와  는 각각 x와 y의 평균입니다.
는 각각 x와 y의 평균입니다.
파라미터 구간추정과 가설 검정
파라미터 구간추정 : 회귀 계수의 신뢰 구간을 추정하여 모델의 신뢰성을 평가합니다.
신뢰 구간 :

여기서 t*는 t-분포의 임계값,  는 표준 오차입니다.
는 표준 오차입니다.
가설 검정 : 회귀 계수가 통계적으로 유의미한지 검정합니다.
- 귀무 가설 (
 ) : β1 = 0 (회귀 계수가 유의미하지 않다)
) : β1 = 0 (회귀 계수가 유의미하지 않다) - 대립 가설 (
 ) : β1 ≠ 0 (회귀 계수가 유의미하다)
) : β1 ≠ 0 (회귀 계수가 유의미하다)
t-검정 :

p-값을 계산하여 귀무 가설을 기각할지 여부를 결정합니다.
정규화 모델
정규화 모델은 과적합을 방지하고 모델의 일반화 성능을 향상시키기 위해 사용됩니다.
릿지 회귀 (Ridge Regression) : 릿지 회귀는 L2 정규화를 사용하여 회귀 계수를 제어합니다.
비용 함수 :

여기서 λ는 정규화 파라미터입니다.
라쏘 회귀 (Lasso Regression) : 라쏘 회귀는 L1 정규화를 사용하여 일부 회귀 계수를 0으로 만듭니다.
비용 함수 :

이 글에서는 회귀분석의 개요, 선형회귀분석의 기본 이해, 경사하강법, 선형회귀모델의 파라미터 추정과 최소제곱법, 파라미터 구간추정과 가설 검정, 정규화 모델에 대해 알아보았습니다. 회귀분석은 데이터를 통해 연속적인 변수를 예측하고, 변수들 간의 관계를 이해하는 데 매우 유용한 기법입니다. 이러한 개념들을 잘 이해하고 활용하면 다양한 문제를 해결하는 데 큰 도움이 될 것입니다.
'인공지능학 > 기계학습' 카테고리의 다른 글
| [기계학습] 6. 군집화의 이해 (0) | 2024.08.06 |
|---|---|
| [기계학습] 5. KNN 알고리즘과 로지스틱 회귀모델 (0) | 2024.08.05 |
| [기계학습] 4. 분류의 이해, Naïve Bayes (0) | 2024.08.01 |
| [기계학습] 2. 기계학습의 수학적 기초 (2) | 2024.07.30 |
| [기계학습] 1. 기계학습의 개요와 주요 유형 (1) | 2024.07.30 |



